消费与储蓄的决定

消费与储蓄的决定

对应书本第7、8讲

储蓄的基本概念

\begin{align*} \text{储蓄} & \equiv \text{收入 $-$ 消费} \\ \text{国民总储蓄} & = \text{GDP $-$ 国民总消费 $=$ GDP $-$ C $-$ G} \\ \text{居民储蓄} & = \text{居民收入 $-$ 居民消费} \\ \text{政府储蓄} & = \text{政府收入 $-$ 政府消费} \\ \text{企业储蓄} & = \text{企业收入 $-$ 企业储蓄 $=$ 企业收入} \end{align*}

Note

!todo

拉姆齐模型(仅居民积累资本)

模型基础设定

  • 两期限模型(two period model)
  • 资本折旧率为0
Tip

内生变量总体可以分为两大类：

  • 控制变量(control variable)，这类取值在当期决定
  • 前定变量(pre-determined variable)，这类取值在上一期被决定,也被称为状态变量(state variable)—-时间下标根据类型而定

居民决策

经济增长的目标是什么，或者什么是评价经济增长的标准

  • 追求更高的人均产出，即人均GDP—-Solow模型
  • 提升居民的福利，也就是提升居民的效用

考虑到模型为两期模型，第二期结束后消费者将消费完所有资源，所以居民的效用偏好函数可以表示为

U = u(c_1)+\beta u(c_2)

其中， 0<\beta<1，\beta为居民的主观贴现因子，说明对于同1单位的消费，今天的消费相比未来的消费可以提升带来更高的效用

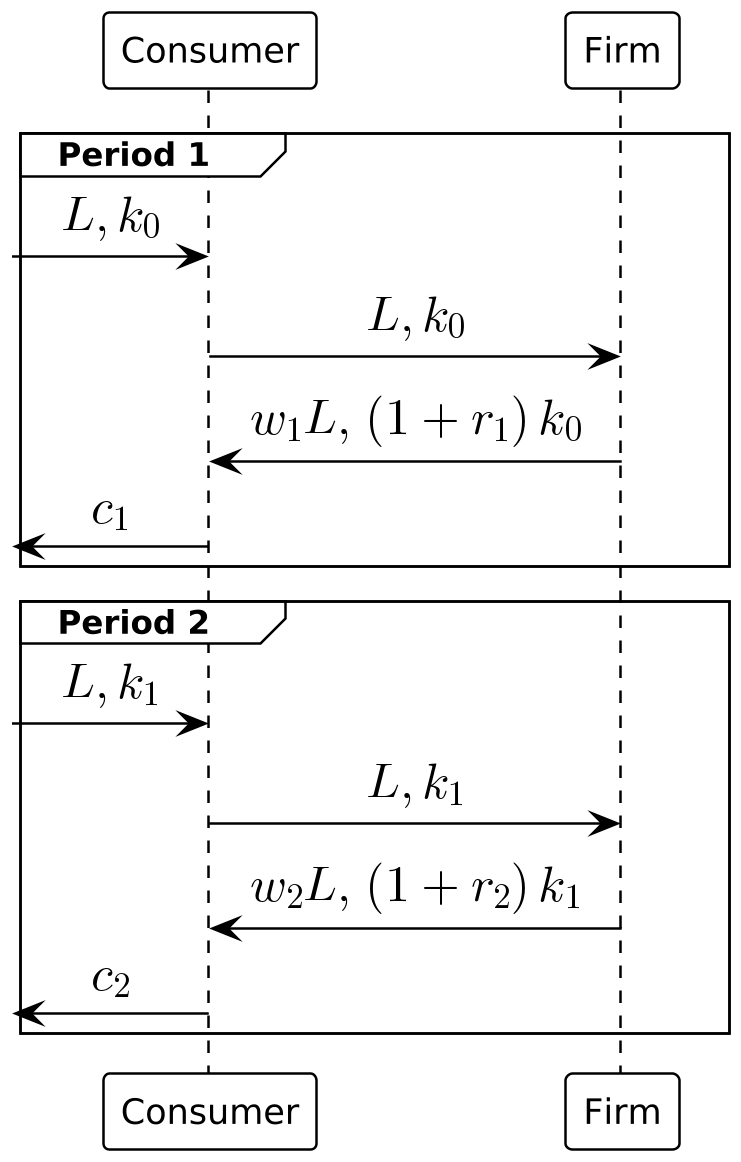
\text{预算约束} \begin{cases} c_1 + k_1 & \le k_0 + w_1L + (1+r_1)k_0 & \text{第1期} \\ c_2 & \le k_1 + w_2L + (1+r_2)k_1 & \text{第2期} \end{cases}

当效用最大化时，两个预算约束条件一定为等式，则可以写成

\begin{align*} \max_{c_1,c_2,k_1} u(c_1) + & \beta u(c_2) \\ \text{s.t.} \quad c_1 + k_1 & = k_0 + w_1L + (1+r_1)k_0 \\ c_2 \qquad & = k_1 + w_2L + (1+r_2)k_1 \\ \end{align*}

设置拉格朗日函数

\mathcal{L} = u(c_1) + \beta u(c_2) + \lambda_1[k_0+w_1L+(1+r_1)k_0-c_1-k_1]+\lambda_2[k_1+w_2L+(1+r_2)k_1-c_2]

对于各内生变量，分别求一阶导后

\begin{align*} \frac{\partial \mathcal{L}}{\partial c_1} = 0 \Rightarrow & u'(c_1) = \lambda_1 \\ \frac{\partial \mathcal{L}}{\partial c_2} = 0 \Rightarrow & \beta u'(c_2) = \Lambda_2 \\ \frac{\partial \mathcal{L}}{\partial k_1} = 0 \Rightarrow & \lambda_1 = \lambda_2(1+r_2) \end{align*}

将拉格朗日乘子消去后得到下式，也可称作欧拉方程(Euler Function)

u'(c_1) = u'(c_2)(1+r_2) (eular-equation)

综上，可以看出欧拉方程是居民消费和储蓄的决策方程。居民的消费储蓄决定于两个要素： 1. 居民两期之间的效用比 u'(c_1)/\beta u'(c_2) 2. 储蓄/资本回报率 r_2

拉姆齐模型 仅居民积累资本的情况

拉姆齐模型 仅居民积累资本的情况

企业决策

由于企业在每期末均进行清算，不进行资本或利润的留存，所以所有储蓄均在消费者处。即，企业每一期的最优化问题可以表达为

\max_{k_{t-1}^d,l_t^d}AF[(k_{t-1}^d,l_t^d) - r_tk_{t-1}^d - w_tl_1^d] \qquad t=1,2

一阶条件分别为

AF_{k_{t-1}^d}(k_{t-1}^d,l_t^d)=r_t \\ AF_{l_1^d}(k_{t-1}^d,l_t^d)=w_t

一般均衡

要达到市场出清(market clear)的情况下，需要以下条件达成

\begin{align*} l_1^d & =l_2^d=L \\ k_o^d & = k_0 \\ k_1^d & = k_1 \end{align*}

将其带入消费者的跨期欧拉方程 {eq}eular-equation、以及消费者的预算约束集后，可以得到

\begin{align*} u'(c_1) \quad & = \beta u'(c_2)[1 + AF_{k_1}(k_1,L)] \\[3ex] c_1 + k_1 & = AF(k_0,L) + k_0 \\ c_2 \qquad & = AF(k_1, L) + k_1 \end{align*}

Note

通过模型可知，消费者最优效用由消费者的主观偏好以及客观世界所能提供的资本回报率同时决定。

Warning

该模型相比于现实存在两个显著的缺陷

  1. 在此模型中，所有的储蓄决策都由消费者做出，模型中企业并未参与。而现实中企业是重要的储蓄/投资的参与者，绝大多数的居民储蓄需要靠企业储蓄转化为投资；同时，企业在每期结束后均会结业清盘，意味着企业只会存活1期，显然也不符合现实情形
  2. 消费者的主观偏好无法预测、度量，那么如何应用于现实呢？

拉姆齐模型(仅企业积累资本)

模型设定

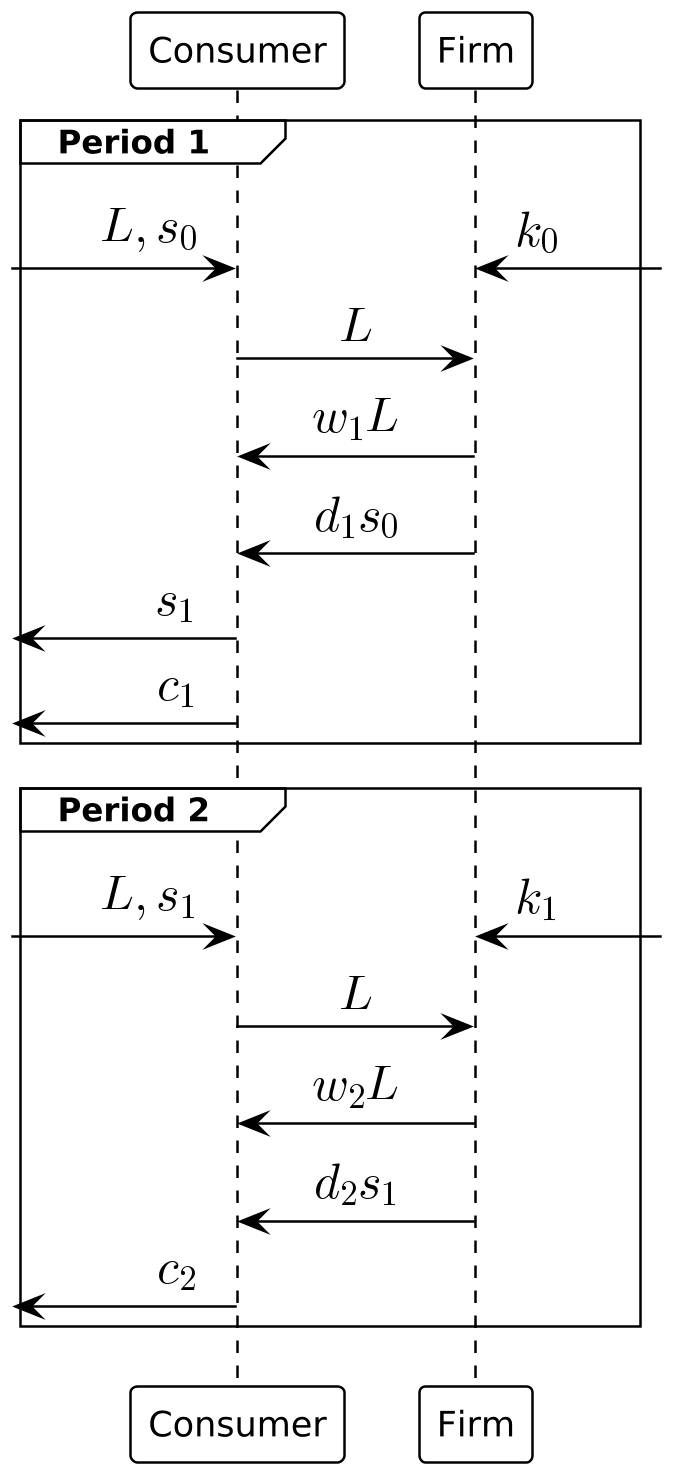
相比之前的模型设定，本此模型中，我们假设模型对应一个私有制社会—-企业为居民所拥有，其股份由居民所持有 具体会有以下的一些不同，可以通过时序图1和时序图2看出:

  1. 居民不再拥有储蓄/资本 k_t ，所以居民也就无法通过向企业借出储蓄/资本以获得的资本回报 r_tk_{t-1}
  2. 居民拥有企业的股份 s_t
    • 居民所持有的股份的价值是 v_ts_{t-1} (v_t为股票价值)
    • 也就意味着居民可以从企业收到所持股份的分红 d_ts_{t-1}
  3. 企业股份的总股数正规化为1， 即 s_0 = s_1 = 1
  4. 企业股权市场充分竞争

其他假设条件：

  1. 待补充

居民决策

Note

第2期中，由于2期末世界毁灭😀，居民所持有的股份价值变为0

居民效用函数仍然维持 u(c_1)+ \beta u(c_2) 这样的形式，约束方面则变为

\text{预算约束} \begin{cases} c_1 + v_1s_1 & \le w_1L + (v_1+d_1)s_0 & \text{第1期} \\ c_2 & \le w_2L + d_2s_1 & \text{第2期} \end{cases}

将以上结合起来，居民的效用最优化问题可以写作

\begin{align*} \max_{c_1,c_2,S_1} u(c_1) + \beta u(c_2) & \\ \text{s.t.} \quad \quad c_1 + v_1s_1 & = w_1L + (v_1+d_1)s_0 \\ c_2 \qquad \quad & = w_2L + d_2s_1 \end{align*}

设置拉格朗日函数

\mathcal{L} = u(c_1) + \beta u(c_2) - \lambda_1[w_1L + (v_1+d_1)s_0 - c_1 - v_1s_1] - \lambda_2[w_2L + d_2s_1 - c_2]

求得一阶导可得

\begin{align*} \frac{\partial \mathcal{L}}{\partial c_1} = 0 \Rightarrow & u'(c_1) = \lambda_1 \\ \frac{\partial \mathcal{L}}{\partial c_2} = 0 \Rightarrow & \beta u'(c_2) = \Lambda_2 \\ \frac{\partial \mathcal{L}}{\partial S_1} = 0 \Rightarrow & \lambda_1v_1 = \lambda_2d_2 \end{align*}

将拉格朗日乘子消去后得到下式

v_1 = \beta \frac{u'(c_2)}{u'(c_1)}d_2 (ramsy-model-only-firm-asset-pricing-equation)

Important

从{eq}ramsy-model-only-firm-asset-pricing-equation可知，资产的价值来自于资产未来可以向所有者提供的现金流

其中，\beta u'(c_2)/u'(c_1) 被称为随机贴现因子(stochastic discount factor)，包含了跨期边际效用比，是 体现了居民主观偏好的一个折现因子

  • 居民主观偏好无法观测，所以该因子无法观测
  • 但同时方程也说明主观偏好可以通过资产价格反推得到

拉姆齐模型 企业积累资本

拉姆齐模型 企业积累资本

企业决策

对于企业，在第2期中，因为第2期后世界毁灭，所以股权价值归为0，消费者为了提升效用将会尽量更多消费，所以消费者将会要求公司将所有资产在支付劳动后，将分红全部给予消费者

其次，对于第1期，企业应该以分红最多为目标，即转化为企业的目标是在分红前将企业股票价值最大化为目标，可以记为 d_1 + v_1 ，如果企业不这么做，那么消费者作为股东会将管理层下岗，或者其他消费者可能会发起敌意并购再炒掉管理层

同时可以参考居民在第1期中的预算约束

c_1 + v_1s_1 \le w_1L + (\color{red}v_1+d_1 \color{black})s_0

其中，居民的预算约束显然受限于企业的分红前股价，为了使居民效用最大化，企业也应该最大化居民的预算约束，即 v_1 + d_1 ，同时，带入{eq}ramsy-model-only-firm-asset-pricing-equation后，可得

d_1 + v_1 = d_1 + \beta \frac{u'(c_2)}{u'(c_1)} d_2

所以，企业的最优化问题可以写为

\begin{align*} \max_{l_1^d, l_2^d, d_1, d_2, k_1} d_1 + \beta & \frac{u'(c_2)}{u'(c_1)} d_2 \\ \text{s.t.} \quad \quad d_1 + k_1 & \le AF(k_0, l_1^d) - w_1l_1^d + k_0 \\ d_2 \qquad & \le AF(k_1, l_2^d) - w_2l_2^d + k_1 \end{align*}

在最优时，约束条件应该是等号，带回最优化目标后，可得

\max_{l_1^d, l_2^d, k_1} AF(k_0, l_1^d) - w_1l_1^d + k_0 - k_1 + \beta \frac{u'(c_2)}{u'(c_1)} [AF(k_1, l_2^d) - w_2l_2^d + k_1]

求一阶导，可得

\begin{align*} \frac{\partial F}{\partial l_1^d} = 0 & \Rightarrow AF_{l_1^d}(k_0, l_1^d) = w_1 \\ \frac{\partial F}{\partial l_2^d} = 0 & \Rightarrow AF_{l_2^d}(k_1, l_2^d) = w_2 \\ \frac{\partial F}{\partial k_1} = 0 & \Rightarrow \beta \frac{u'(c_2)}{u'(c_1)} [AF_{k_1}(k_1, l_2^d) + 1] = 1 \end{align*}

一般均衡

在均衡时，可知有条件 $ l_1^d = l_2^d = L, s_1 = s_0 = 1 $, 上式可简化为

u'(c_1) = \beta u'(c_2)[AF_{k_1}(k_1, L) + 1]

对比拉姆齐模型（仅居民积累资本）中的均衡条件，完全相同。

:name: piercing-the-corporate-veil
`刺穿企业帷幕(piercing the corporate veil)`

以上模型说明，在居民拥有企业股权时，居民储蓄或企业储蓄效果相同，股票价格由居民决定，股票价值最大化，同时也意味着居民效用最大化，故`居民与企业两部门之间的收入分配变化不影响居民的消费与储蓄决策`

模型求解的三点技术注释

  1. 居民优化问题中企业股份的选择
    • 微观层面
    • 宏观层面
  2. 企业的优化目标函数
    • 间接联系 or 直接联系，通过价格 or 直接控制
    • 微观层面
    • 宏观层面
  3. 均衡求解
    • 取决于模型构造的目的，结果or结论？

拉姆齐模型(居民与企业同时积累资本)

模型设定

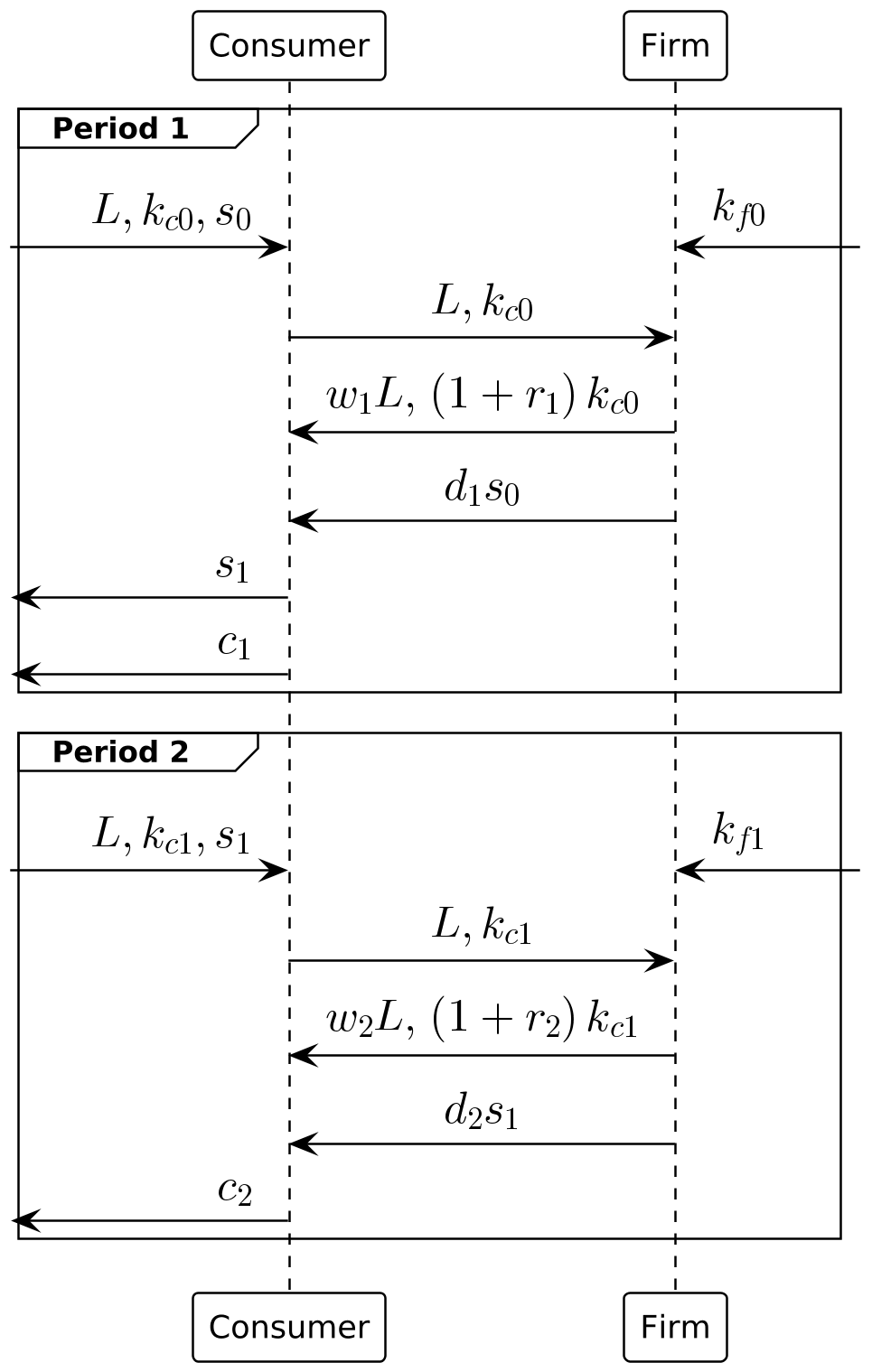
  1. 沿用之前的私有制社会设定—-企业为居民所拥有，其股份由居民所持有，世界依然在第2期毁灭
  2. 居民和企业同时持有储蓄，对于t期期初，可分别标记为 k_{ct} 以及 k_{ft} ，同时假定第1期期初储蓄总量为常量 $ k_0 k_{c0} + k_{f0}$
  3. 居民拥有企业的股份 s_t
    • 居民所持有的股份的价值是 v_ts_{t-1} (v_t为股票价值)
    • 也就意味着居民可以从企业收到所持股份的分红 d_ts_{t-1}
    • 1期分红后，居民可以 v_1 价格交易股份，期末持有 s_1 单位
  4. 宏观层面，企业股份的总股数正规化为1， 即 s_0 = s_1 = 1

居民决策

显然，居民效用函数仍然维持 u(c_1)+ \beta u(c_2) 这样的形式，约束方面则变为

\text{预算约束} \begin{cases} c_1 + k_{c1} + v_1s_1 & \le w_1L + (1+r_1)k_{c0} + (v_1+d_1)s_0 & \text{第1期} \\ c_2 & \le w_2L + (1+r_2)k_{c1} + d_2s_1 & \text{第2期} \end{cases}

将以上结合起来，则居民的效用最优化问题可以写作

\begin{align*} \max_{c_1,c_2, k_{c1},s_1} u(c_1) + \beta u(c_2) & \\ \text{s.t.} \quad \quad c_1 + k_{c1} + v_1s_1 & \le w_1L + (1+r_1)k_{c0} + (v_1+d_1)s_0 \\ c_2 \hspace{54pt} & \le w_2L + (1+r_2)k_{c1} + d_2s_1 \end{align*}

目标函数最优时约束条件取等号，设定拉格朗日函数

\mathcal{L} = u(c_1) + \beta u(c_2) + \lambda_1[w_1L + (1+r_1)k_{c0} + (v_1 + d_1)s_0 - c_1 - k_{c1} - v_1s_1] + \lambda_2[w_2L + (1+r_2)k_{c1} + d_2s_1 - c_2]

求一阶导，可得

\begin{align*} \frac{\partial F}{\partial c_1} = 0 & \Rightarrow u'(c_1) = \lambda_1 \\ \frac{\partial F}{\partial c_2} = 0 & \Rightarrow \beta u'(c_2) = \lambda_2 \\ \frac{\partial F}{\partial k_{c1}} = 0 & \Rightarrow \lambda_1 = \lambda_2(1 + r_2) \\ \frac{\partial F}{\partial s_1} = 0 & \Rightarrow \lambda_1v_1 = \lambda_2d_2 \end{align*}

通过消去拉格朗日乘子，可得

\begin{align*} v_1 & = \beta \frac{u'(c_2)}{u'(c_1)}d_2 \\ 1 & = \beta \frac{u'(c_2)}{u'(c_1)}(1+r_2) \end{align*}

两个等式分别对应股票和资产的定价方程，通过替换随机贴现因子，可以得到无套利条件：股权收益率应等于资本租借的收益率

\frac{v_2}{d_1} = 1 + r_2

拉姆齐模型 同时积累资本

拉姆齐模型 同时积累资本

企业决策

对于企业而言，企业的最优化目标仍然是第1期分红前的股价最大化，即 v_1 + d_1 ，同时最优化目标通过变化后也可以表达为两期贴现和最大值，即

d_1 + v_1 = d_1 + \beta \frac{u'(c_2)}{u'(c_1)} d_2

所以，企业的最优化问题可以记作

\begin{align*} \max_{l_1^d, l_2^d, k_0^d, k_1^d, k_{f1}} d_1 + \beta & \frac{u'(c_2)}{u'(c_1)} d_2 \\ \text{s.t.} \quad \quad d_1 + k_{f1} & \le AF(k_{f0} + k_0^d, l_1^d) - w_1l_1^d - r_1k_0^d + k_{f0} \\ d_2 \hspace{25pt} & \le AF(k_{f1} + k_1^d, l_2^d) - w_2l_2^d - r_2k_1^d + k_{f1} \end{align*}

Caution

暂时不太懂为什么这个地方的内生变量中是 k_0^d 和 k_1^d

在最优时，约束条件应该是等号，带回最优化目标后，可得

\max_{l_1^d, l_2^d, k_0^d, k_1^d, k_{f1}} [AF(k_{f0} + k_0^d, l_1^d) - w_1l_1^d - r_1k_0^d + k_{f0} - k_{f1}] + \beta \frac{u'(c_2)}{u'(c_1)}[AF(k_{f1} + k_1^d, l_2^d) - w_2l_2^d - r_2k_1^d + k_{f1}]

求一阶导，可得

\begin{align*} \frac{\partial F}{\partial l_1^d} = 0 \quad & \Rightarrow \quad AF_{l_1^d}(k_{f0} + k_0^d, l_1^d) = w_1 \\ \frac{\partial F}{\partial l_2^d} = 0 \quad & \Rightarrow \quad AF_{l_2^d}(k_{f1} + k_1^d, l_2^d) = w_2 \\ \frac{\partial F}{\partial k_0^d} = 0 \quad & \Rightarrow \quad AF_{k_0^d}(k_{f0} + k_0^d, l_1^d) = r_1 \\ \frac{\partial F}{\partial k_1^d} = 0 \quad & \Rightarrow \quad AF_{k_1^d}(k_{f1} + k_1^d, l_2^d) = r_2 \\ \frac{\partial F}{\partial k_{f1}} = 0 \quad & \Rightarrow \quad 1 = \beta \frac{u'(c_2)}{u'(c_1)}[AF_{k_{f1}}(k_{f1} + k_1^d, l_2^d) + 1] \end{align*}

一般均衡

均衡时，劳动力、资本及股权市场全部出清，故有

\begin{align*} & l_1^d = l_2^d = L \\ & k_0^d = k_0, k_1^d = k_1 \\ & s_0 = s_1 = 1 \end{align*}

同时有设定 k_0 \equiv k_{c0} + k_{f0} ，再定义 k_1 \equiv k_{c1} + k_{f1} ，代入一阶导后，可得

\begin{align*} & AF_{l_1^d}(k_0, L) = w_1 & AF_{l_2^d}(k_1, L) = w_2 \\ & AF_{k_0^d}(k_0, L) = r_1 & AF_{k_1^d}(k_1, L) = r_2 \end{align*}

考虑总体均衡时，居民部门在两期持有的股份数相同，都是1，通过变换居民和企业的预算约束，可以得到

\begin{align*} & c_1 + k_{c1} & = & w_1L + (1+r_1)k_{c0} + d_1 \\ & c_2 & = & w_2L + (1+r_2)k_{c1} + d_2 \\[3ex] & d_1 + k_{f1} & = & AF(k_0, L) - w_1L - r_1k_0 + k_{f0} \\ & d_2 & = & AF(k_1, L) - w_2L - r_2k_1 + k_{f1} \end{align*}

通过消去 d_1 和 d_2 ，可得等式，正好是两期中消费品市场出清的条件

\begin{align*} & c_1 = AF(k_0,L) + k_0 - k_1 \\ & c_2 = AF(k_1,L) + k_1 \end{align*}

同时，将居民优化中的资本定价方程可以化为

1 = \beta \frac{u'(c_2)}{u'(c_1)}(1+r_2) = \beta \frac{u'(c_2)}{u'(c_1)}[1+ AF_{k_1}(k_1, L)]

综合上面三个式子，可得

\begin{cases} u'(c_1) & = \beta u'(c_2)[1+ AF_{k_1}(k_1, L)] \\ c_1 +k_1 & = AF(k_0,L) + k_0 && \text{1期资源总约束} \\ c_2 & = AF(k_1,L) + k_1 && \text{2期资源总约束} \end{cases}

对储蓄的分析

储蓄的定义

首先，第1期社会总储蓄

saving = AF(k_0, L) - c_1 = k_1 - k_0

第1期中单个居民的预算约束可以表示为居民收入减去居民消费

saving_c^{Micro} = r_1k_{c0} + w_1L + d_1s_0 - c_1 = (k_{c1} - k_{c_0}) + (v_1s_1 - v_1s_0) \tag{1}

通过将居民预算约束变形可得出

saving_c = r_1k_{c0} + w_1L + d_1 - c_1 = k_{c1} - k_{c0} \tag{2}

Proof (如何理解居民储蓄在微观层面以及宏观层面的两个等式).

  1. 微观层面到宏观层面的思路
    • 微观等式 Equation 1 来说，居民的储蓄被用于两方面：
      • 资本的增量
      • 股份的增量
    • 宏观等式 Equation 2 来说，居民的储蓄仅被用于资本的增量这一用途
    • 这种差异是因为企业所有权均由居民持有，假设居民宏观层面增加或减少持股数，则企业所有权市场显然处于未出清状态，所以居民在跨期中并未变动总持股量，所以这样就导致在宏观层面，居民的储蓄仅被用于了资本增量
  2. 注意区分微观变量与宏观变量
    • 微观等式 Equation 1 和宏观等式 Equation 2 中 d_1 的系数相对特殊，微观等式中为 s_0 。而宏观等式中为 1 。其实微观和宏观等式中系数即便相同，其含义也是不同的

如{eq}consumer-saving-macro-equation，通过对企业预算约束等式进行变换，则可得到企业部门的储蓄表达式

saving_f = AF(k_0, L) - w_1L - r_1k_0 - d_1 = k_{f1} - f_{f0} (firm-saving-macro-equation)

将居民的储蓄等式{eq}consumer-saving-macro-equation和企业的储蓄等式{eq}firm-saving-macro-equation相加后可得

saving_c + saving_f = k_{c1} - k_{c0} + k_{f1} - k_{f0} = (k_{c1} + k_{f1}) - (k_{c0} + k_{f0}) = k_1 - k_0

居民与企业总储蓄仅与宏观变量 k_1 有关，这无疑验证了{ref}刺穿企业帷幕<piercing-the-corporate-veil>理论

总储蓄和净储蓄

总储蓄(gross saving)
部门的收入 - 消费
净储蓄(net saving)
部门的总储蓄 - 投资

资金总是从净储蓄为正的部门流向净储蓄为负的部门。若将概念运用于国家层面，国家总储蓄与总投资之间的缺口需要国家贸易及国际资本流动解决。一个国家如果有正的净储蓄需要借给外国，则其表现为产品和服务的净流出国，因而形成经常账户(current account)的顺差

\begin{align*} S &= Y - C \\ S_{net} &= S - I \\ CA &= S - I = S_net \end{align*}

现实中消费与储蓄如何决定

居民角度

消费者想要最大化效用 U，而因为今天和明天同1单位消费的效用是不同的，所以对于两期模型，最大化效用可以表达为 U(c_1) + \beta U(c_2) ，其中 0< \beta < 1

  • 因为人性不耐，所以未来的效用需要贴现（打折扣）
  • 消费者通过选择消费或储蓄来达到效用最大化
    • 消费在每一期的边际效用是逐步递减的，所以消费需要在各期尽量平滑分布
    • 通过储蓄，消费者可以在不同期之间转移消费，以实现消费的平滑分布
Note

最优消费/储蓄的状态是指消费者在消费的主观偏好与资本回报率之间的平衡，也就是消费者跨期效用比与资本回报率之间的平衡。

图形解释

TBD

企业的分红可能性边界

消费者的主观时间偏好

企业所有权竞争市场中的企业与消费者

再论萨伊定律及总结

萨伊定律认为宏观经济中不太可能出现生产过剩及就业不足，反映了起对市场高效运作的信心 - 生产是因为需求已经在之前产生 - bug：生产可能一部分是出于储蓄动机

最优消费储蓄在真实世界实现的前提条件 - 企业所有权归居民所有 - 企业所有权市场（资本市场）是竞争市场

实现机制 - 资本市场中消费者通过股权的定价来体现出对资产回报率的要求，同时也反映出跨期效用比 - 投资回报率是企业所有权向消费者提供的回报率 - 两者形成均衡 - 投资较多，资本回报率下降，消费者将要求企业增加分红，资本流向消费者 - 投资较少，资本回报率较高时，消费者将追加投资

Tip

所以，实际上拉姆齐模型实际上隐含着萨伊定律的成立，这也意味着该模型情况下，经济增长的瓶颈在于供给面，而非需求面。

中国消费和储蓄的基本事实

TBD

模型与中国经济的数量分析

TBD

补充：多期模型的扩展

补充：理性预期

TBD

课后练习

问题1

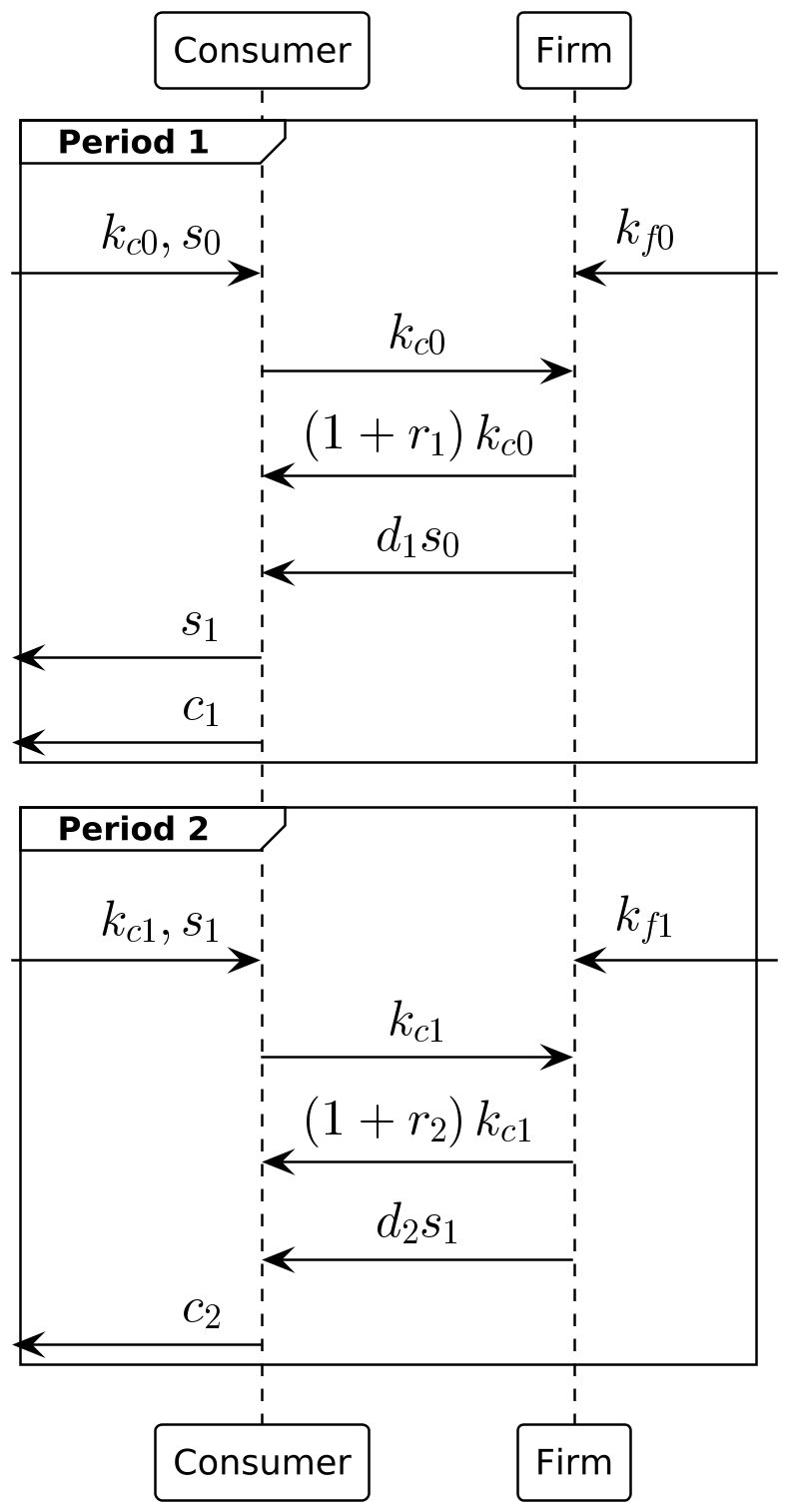
拉姆齐两期模型中，嘉定企业的生产函数为 y=k^{0.5} （生产不需要劳动力），全社会在第1期期初的资本存量为1。在第1期期初全社会的总资本中，有一半属于居民，一半属于企业，并且企业所有权在居民手中

  1. 请画出模型的时序图
  2. 定义模型均衡
  3. 求解均衡时居民两期的消费量以及第2期的资本回报率

题1 时序图

题1 时序图

居民方面：

居民的效用最大化目标函数及约束条件是

\max_{c_1,c_2,s_1,k_{c1}} u(c_1) + \beta u(c_2) \hspace{60pt} \\[2ex] \begin{align*} & c_1 + k_{c1} + v_1s_1 & \le & (1 + r_1)k_{c0} + d_1s_0 + v_1s_0 \\ & c_2 & \le & (1 + r_2)k_{c1} + d_2s_1 \end{align*}

在目标函数达到最优化时，约束条件取等号，设置拉格朗日函数，可得

\mathcal{L} = u(c_1) + \beta u(c_2) + \lambda_1[(1 + r_1)k_{c0} + d_1s_0 + v_1s_0 - c_1 - k_{c1} - v_1s_1] + \lambda_2[(1 + r_2)k_{c1} + d_2s_1 - c_2]

取一阶导数，可得

\begin{align*} \frac{\partial F}{\partial c_1} = 0 & \Rightarrow u'(c_1) = \lambda_1 \\ \frac{\partial F}{\partial c_2} = 0 & \Rightarrow \beta u'(c_2) = \lambda_2 \\ \frac{\partial F}{\partial k_{c1}} = 0 & \Rightarrow \lambda_1 = \lambda_2(1 + r_2) \\ \frac{\partial F}{\partial s_1} = 0 & \Rightarrow \lambda_1v_1 = \lambda_2d_2 \end{align*}

消去拉格朗日乘子，可得

\begin{align*} 1 &= \beta \frac{u'(c_2)}{u'(c_1)} (1+r_2) \\ v_1 &= \beta \frac{u'(c_2)}{u'(c_1)} d_2 \end{align*}

企业方面：

企业的效用最大化目标函数及约束条件是

\max_{k_0^d, k_1^d, k_{f1}} v_1 + d_1 \hspace{40pt} \\[2ex] \begin{align*} & k_{f1} + d_1 & \le & F(k_{f0} + k_0^d) - r_1k_0^d + k_{f0} \\ & d_2 & \le & F(k_{f1} + k_1^d) - r_2k_1^d + k_{f1} \end{align*}

在目标函数最优化时，约束条件应该取等号，将消费者及企业约束条件分别带入目标函数，可得

\begin{align*} \max_{k_0^d, k_1^d, k_{f1}} v_1 + d_1 & = \beta \frac{u'(c_2)}{u'(c_1)} d_2 + d_1 \\ & = \beta \frac{u'(c_2)}{u'(c_1)} [F(k_{f1} + k_1^d) - r_2k_1^d + k_{f1}] + [F(k_{f0} + k_0^d) - r_1k_0^d + k_{f0} - k_{f1}] \end{align*}

取一阶导，可得

\begin{align*} \frac{\partial F}{\partial k_0^d} = 0 \quad & \Rightarrow \quad F'(k_{f0} + k_0^d) = r_1 \\ \frac{\partial F}{\partial k_1^d} = 0 \quad & \Rightarrow \quad F'(k_{f1} + k_1^d) = r_2 \\ \frac{\partial F}{\partial k_{f1}} = 0 \quad & \Rightarrow \quad 1 = \beta \frac{u'(c_2)}{u'(c_1)}[F'(k_{f1} + k_1^d) + 1] \end{align*}

均衡分析：

均衡时，劳动力、资本、企业所有权市场应该处于出清状态，可知一下等式成立

\begin{align*} k_0^d &= k_{c0} \\ k_1^d &= k_{c1} \\ s_1 &= s_0 = 1 \end{align*}

则企业优化条件可以转换为

\begin{align*} \frac{\partial F}{\partial k_0^d} = 0 \quad & \Rightarrow \quad F'(k_0) = r_1 \\ \frac{\partial F}{\partial k_1^d} = 0 \quad & \Rightarrow \quad F'(k_1) = r_2 \\ \frac{\partial F}{\partial k_{f1}} = 0 \quad & \Rightarrow \quad 1 = \beta \frac{u'(c_2)}{u'(c_1)}[F'(k_1) + 1] \end{align*}

均衡时，由于企业部门在两期持有的股票数量不变，均为1，则居民部门在最优时的预算约束可变形为

\begin{align*} & c_1 + k_{c1} &= (1 + r_1)k_{c0} + d_1 \\ & c_2 &= (1 + r_2)k_{c1} + d_2 \end{align*}

企业部门最优化的约束条件可以变换为

\begin{align*} & k_{f1} + d_1 & = F(k_0) - r_1k_{c0} + k_{f0} \\ & d_2 & = F(k_1) - r_2k_{c1} + k_{f1} \end{align*}

将变换后的企业约束条件带入居民部门的约束条件等式，消去 d_1 和 d_2 ，可得

\begin{align*} & c_1 + k_{c1} &=& (1 + r_1)k_{c0} + F(k_0) - r_1k_{c0} + k_{f0} - k_{f1} &=& F(k_0) + k_0 -k_{f1} \\ & c_2 &=& (1 + r_2)k_{c1} + F(k_1) - r_2k_{c1} + k_{f1} &=& F(k_1) +k_1 \end{align*}

所以，综合以上居民部门约束条件以及企业的欧拉方程，可得到均衡状态的条件是

\begin{cases} c_1 + k_{c1} &= F(k_0) + k_0 -k_{f1} \\ c_2 &= F(k_1) +k_1 \\ u'(c_1) &= \beta u'(c_2)[F'(k_1) + 1] \end{cases}

我们将居民效用函数取为 CRRA 形式，即为

U = \frac{c_1^{1- \sigma}}{1 - \sigma} + \beta \frac{c_2^{1- \sigma}}{1 - \sigma}

根据一般情况， \sigma 作为居民的相对风险规避系数，一般取值为2， \beta 作为消费者主观贴现因子，根据宏观惯例一般取值是0.98，则居民效用函数具体为

U = - \frac{1}{c_1} - \frac{0.98}{c_2}

根据条目给定条件，可知有一下条件等式成立

\begin{align*} F(k) = k^{0.5} \\ k_{c0} + k_{f0} = k_0 = 1 \\ k_{c0} = k_{f0} = 0.5 \end{align*}

将条件带入均衡状态条件组后，结合企业的优化条件，可得

\begin{cases} c_1 &= F(k_0) + k_0 -k_{f1} - k_{c1} = 1^{0.5} + 1 - k_1 = 2 -k_1 \\ c_2 &= F(k_1) +k_1 = k_1^{0.5} + k_1 \\ u'(c_1) &= \beta u'(c_2)[F'(k_1)+1] = \beta u'(c_2)(0.5k_1^{-0.5} + 1) \end{cases}

整理后可得

\begin{cases} c_1 & = 2 -k_1 \\ c_2 & = k_1^{0.5} + k_1 \\ (\frac{c_2}{c_1})^2 & = 0.98 (0.5k_1^{-0.5} + 1) \end{cases}

通过变换条件，将方程组变为 k_1 的一元方程，通过以下python代码求解

from scipy.optimize import root

def func(x):
    return (( (x**0.5 + x)/(x-2) )**2 - 0.98 * (0.5 * (x**-0.5) + 1))**2

sol = root(func, 1)
k = sol.x[0]
c1 = 2 - k
c2 = k**0.5 + k
r2 = 0.5 * (k**-0.5)

通过代码求解，可解得一期消费c_1为1.2705，二期消费c_2为1.5836， 一期期末总资本k_1为0.7295。二期资本收益率r_2为58.54%

Caution

以下几个小问题可以帮助大家熟悉储蓄的概念

  1. 海解释以下几个概念：国民总储蓄、居民储蓄、企业储蓄、政府储蓄
  2. 请列举出以上几个概念在真实世界中的具体表现北式（无须穷尽，指出几个例子即可。如，居民的银行存款是居民储蓄的一种表现形式）
  3. 请查找最近一年的宏观统计数据，计算以上几个概念对应的指标占中国当年 GDP 的比重。（提示：在中国国家统计局每年发布的中国资金流量表（实物部分）中可以找到这些数据）
  4. 请计算不包含中国的全球经济储蓄率（国民总储蓄占 GDP 的比重），并将其与中国的储蓄率做对比。从中你能得到什么样的启示？[提示：在国际货币基金组织（IMF)的国际经济展望数据库 (World Economic Outlook Database）中可以查到相关数据]
Caution

你认为萨伊定律在中国成立吗？请论述你的论点、逻辑和证据。

Tip

结论是萨伊定律在中国不能成立。